隐马尔可夫链

Hidden Markov Model (HMM)

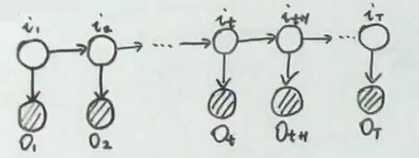
变量说明

\(I=i_1,i_2,...,i_T\) → 状态序列

\(Q=\{q_1,q_2,...,q_N\}\) → 状态值集合

\(O=o_1,o_2,o_3,...,o_T\) → 观测序列

\(V={v_1,v_2,...,v_M}\) → 观测值集合

参数说明

\(\lambda=(\pi,A,B)\)

\(\pi=(\pi_1,\pi_2,...,\pi_N)\)，\(\pi_i=P(i_1=q_i)\) 且 \(\sum\limits_{i=1}^{M}{\pi_i}=1\) → 初始概率分布

\(A: [a_{ij}]\)，其中 \(a_{ij}=P(i_{t+1}=q_j|i_t=q_i)\) → 转移矩阵

\(B: [b_j(k)]\)，其中 \(b_j(k)=P(o_{t}=v_k|i_t=q_j)\) → 发射矩阵

两个假设

① 齐次马尔可夫规则

\(P(i_{t+1}|i_1,...,i_t,o_1,...,o_t)=P(i_{t+1}|i_t)\)

② 观测独立原则

\(P(o_t|i_1,...,i_t,o_1,...,o_t)=P(o_t|i_t)\)

学习任务推导证明

对于HMM来说，学习任务指的是从训练集中学习HMM的参数 \(\lambda\) ，转化为数学问题为 \(\lambda_{MLE}=\underset{\lambda}{argmax}\ P(O|\lambda)\) 。所使用的方法为 Baum–Welch 算法（EM算法的变体）。

根据EM算法的公式，即

\[ \theta^{(t+1)}=\underset{\theta}{argmax}\ \int_Z\log{P(X,Z|\theta)}P(Z|X,\theta^{(t)}) \mathrm{d} z \]

其中，\(X\) 为观测值，\(Z\) 为隐变量，\(\theta\) 为参数。

根据HMM中定义的符号替换上式的对应符号，可以得到下式：

\[ \lambda^{(t+1)}=\underset{\lambda}{argmax}\ \sum\limits_{I}\log{P(O,I|\lambda)}P(I|O,\lambda^{(t)}) \]

由于 \(P(I|O,\lambda^{(t)})=\frac{P(I,O|\lambda^{(t)})}{P(O,\lambda^{(t)})}\)，且此时 \(\lambda^{(t)}\) 为常数，因此，可以用 \(P(I,O|\lambda^{(t)})\) 替代 \(P(I|O,\lambda^{(t)})\)，得到：

\[ \lambda^{(t+1)}=\underset{\lambda}{argmax}\ \sum\limits_{I}\log{P(O,I|\lambda)}P(O,I|\lambda^{(t)}) \]

其中，\(\lambda^{(t)}=(\pi^{(t)},A^{(t)},B^{(t)})\)。

根据HMM的定义，可以得到

\[ P(O|\lambda)=\sum\limits_{I}P(O,I|\lambda)=\sum\limits_{i_1}...\sum\limits_{i_T}\pi_{i_1}\prod\limits_{t=2}^Ta_{i_{t-1}i_t}\prod\limits_{t=1}^{T}b_{i_t}(o_t) \]

联立前两式，可以得到优化函数为

\[ Q(\lambda,\lambda^{(t)})=\sum\limits_{I}\log{P(O,I|\lambda)}P(O,I|\lambda^{(t)})=\sum\limits_{I}[\log\pi_{i_1}+\sum\limits_{t=2}^T\log a_{i_{t-1}i_t}+\sum\limits_{t=1}^{T}\log b_{i_t}(o_t)]P(O,I|\lambda^{(t)}) \]

下面以 \(\pi\) 为例，推导参数的计算，参数 \(A\) 和 \(B\) 同理。

由上面的推导有，

\[ \begin{align*} \pi^{(t+1)} &=\underset{\pi}{argmax}\ Q(\lambda,\lambda^{(t)}) =\underset{\pi}{argmax}\sum\limits_{I}[\log\pi_{i_1}P(O,I|\lambda^{(t)})] \\ &=\underset{\pi}{argmax}\sum\limits_{i_1}...\sum\limits_{i_T}[\log\pi_{i_1}P(O,i_1,...,i_T|\lambda^{(t)})] =\underset{\pi}{argmax}\sum\limits_{i_1}[\log\pi_{i_1}P(O,i_1|\lambda^{(t)})] \end{align*} \]

由于 \(i_1\) 为初始状态，且 \(i_1\) 的取值范围为 \(Q=\{q_1,q_2,...,q_N\}\)，所以上式可以进一步写为

\[ \pi^{(t+1)} =\underset{\pi}{argmax}\sum\limits_{i=1}^N[\log\pi_{i}P(O,i_1=q_i|\lambda^{(t)})]\\ \mathrm{ s.t. } \sum\limits_{i=1}^N\pi_i=1 \]

观察上式，发现可以使用拉格朗日乘子法求解该优化方程。定义拉格朗日乘子法的函数为

\[ \mathcal{L}(\pi, \eta)=\sum\limits_{i=1}^N[\log\pi_{i}P(O,i_1=q_i|\lambda^{(t)})]+\eta(\sum\limits_{i=1}^N\pi_i=1) \]

对 \(\pi_i\) 求偏导，令偏导为0，可以得到

\[ \frac{\partial \mathcal{L}}{\partial \pi_i}=\frac{1}{\pi_i}P(O,i_1=q_i|\lambda^{(t)})+\eta=0 \\ \Rightarrow P(O,i_1=q_i|\lambda^{(t)})+\pi_i\eta=0\\ \Rightarrow \sum\limits_{i=1}^{N}[P(O,i_1=q_i|\lambda^{(t)})+\pi_i\eta]=0\\ \Rightarrow P(O|\lambda^{(t)})+\eta=0\\ \Rightarrow \eta = -P(O|\lambda^{(t)}) \]

将 \(\eta =-P(O|\lambda^{(t)})\) 代回等式，得到

\[ \pi_i^{(t+1)}=\frac{P(O,i_1=q_i|\lambda^{(t)})}{P(O|\lambda^{(t)})} \]

同理可以得到，\(\pi^{(t+1)}=(\pi_1^{(t+1)},\pi_2^{(t+1)},...,\pi_N^{(t+1)})\) 的表达式。

至此，建立了 \(\pi^{(t+1)}\) 和 \(\lambda^{(t)}\)的关系式，即建立了\(\pi^{(t+1)}\)与 \(\pi^{(t)}\)的关系式，满足了EM算法的条件。参数 \(A\) 和 \(B\) 的计算推导同理，不再赘述。

综上所述，推导证明HMM算法参数学习的数学原理可行。