双目成像相关原理

基本原理

双目深度相机基本原理

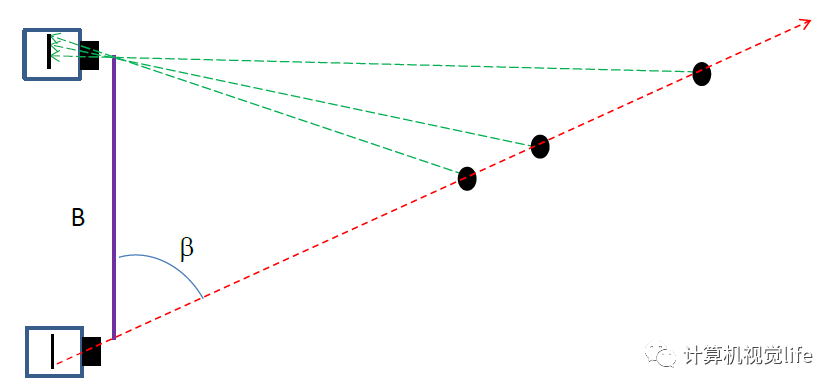
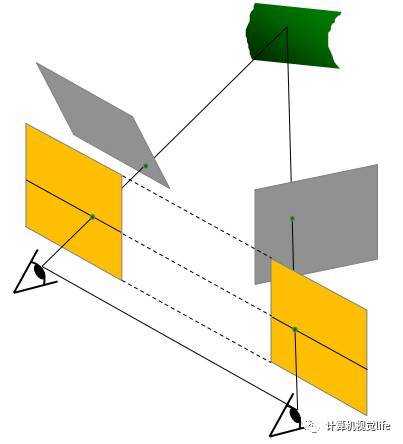
下图从物理原理上展示了为什么单目相机不能测量深度值而双目可以。我们看到红色线条上三个不同远近的黑色的点在下方相机上投影在同一个位置，因此单目相机无法分辨成的像到底是远的那个点还是近的那个点，但是它们在上方相机的投影却位于三个不同位置，因此通过两个相机的观察可以确定到底是哪一个点。

双目深度相机基本流程

1. 首先需要对双目相机进行标定，得到两个相机的内外参数、单应矩阵；

2. 根据标定结果对原始图像校正，校正后的两张图像位于同一平面且互相平行；

3. 对校正后的两张图像进行像素点匹配；
4. 根据匹配结果计算每个像素的深度，从而获得深度图。

---

详细原理

理想双目相机模型

理想模型：① 左右两个相机位于同一平面（光轴平行）；② 左右相机参数（如焦距 \(f\) 等）一致。推导如下图所示。

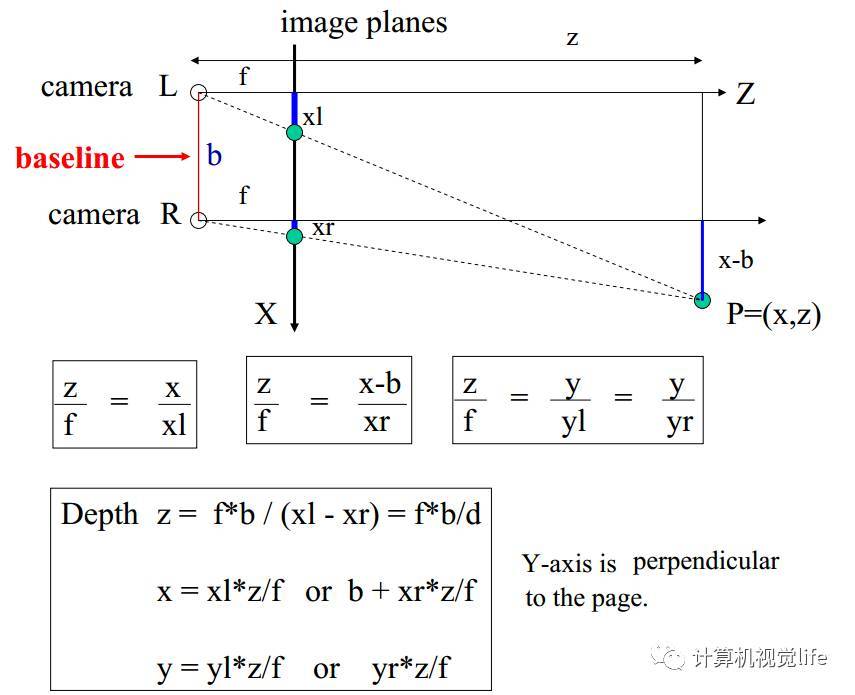
根据以上推导，得到三维空间中一点 \(P\) 的深度为 \(z=f*b/d\) ，可以发现如果要计算深度 \(z\)，必须要知道：

1. 相机焦距 \(f\) 和 左右相机基线 \(b\) —— 可通过先验信息或相机标定得到；
2. 视差 \(d\) —— 需要知道左相机的任一像素点 \((xl, yl)\) 和右相机中对应点 \((xr, yr)\) 的对应关系。

---

极线约束定理

问：对于左图中的一个像素点，如何确定该点在右图中的位置？是不是需要我们在整个图像中地毯式搜索一个个匹配？

答：不需要。根据 极线约束 ，可以极大地缩小匹配范围。

极平面与极线

如下图所示，C1，C2是两个相机，P是空间中的一个点，P和两个相机中心点C1、C2形成了三维空间中的一个平面PC1C2，称为 极平面 （Epipolar plane）。极平面和两幅图像相交于两条直线，这两条直线称为 极线 （Epipolar line）。

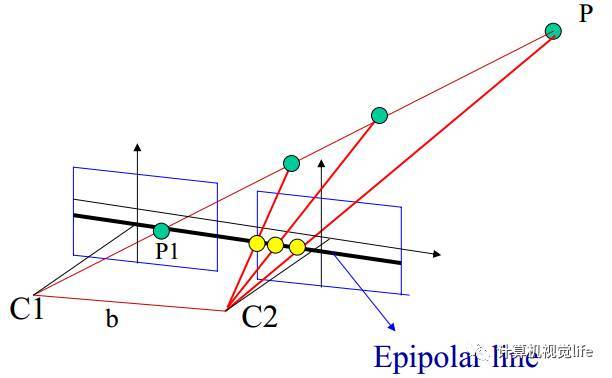
极线约束定理

如上图所示，假设P在相机C1中的成像点是P1，在相机C2中的成像点是P2，但是P的位置事先是未知的。对于左图的P1点，我们希望找到它在右图中对应的P2点。 极线约束（Epipolar Constraint） 是指： 当同一个空间点P在两幅图像上分别成像时，已知左图投影点P1，那么对应右图投影点P2一定在相对于P1点的极线上 。根据极线约束的规律，我们只需要沿着极线搜索就一定可以找到和P1的对应点P2。

极线的获取

已知P1点，可以确定平面P1C1C2，易知该平面与极平面PC1C2重合；计算平面P1C1C2与右相机图像的交线，即为相对于P1的极线。

---

图像矫正

非理想情况

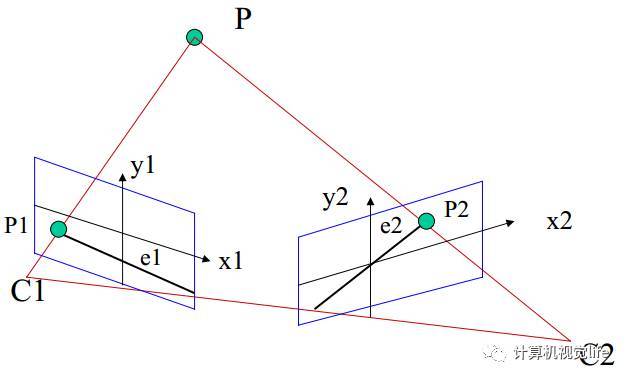
上述过程考虑的情况（两相机共面且光轴平行、参数相同）非常理想，但如果相机C1，C2不是在同一直线上怎么办？事实上，这种情况非常常见，因为有些场景下两个相机需要独立固定，很难保证光心C1，C2完全水平，即使是固定在同一个基板上也会因为装配的原因导致光心不完全水平。如下图a所示，当两个相机的极线不平行且不共面时，根据理想模型推导的公式不能直接使用。而且在非理想的情况下，如下图b中的所示，左图中任一点对应到右图的极线为斜线，此时逐点搜索的效率非常低。

图a：非理想情况相机模型示意图	图b：左图中三个点（十字标志）在右图中对应的极线是右图中的三条白色直线

图像矫正

对于非理想情况下（也即一般情况下），我们需要通过 图像矫正（Image Rectification） 将图像转化为理想模型。图像矫正是通过分别对两张图片用 单应矩阵（homography matrix） 变换（可以通过 标定 获得）得到的，目的就是把两个不同方向的图像平面（图a中灰色平面）重新投影到同一个平面且光轴互相平行（图a中黄色平面），两个相机的极线也变成水平的。如图b所示，我们可以看到三个点对应的视差是不同的，越远的物体视差越小，越近的物体视差越大，这和我们的常识是一致的。

图a：图像矫正示意图	图b：图像矫正后的结果示意图；红色双箭头线段是对应点的视差

---

相机标定

相关坐标系

物体的三维信息都是通过二维图像推导而来的。要想明确物体在三维空间的具体位置，除了图像的信息，还需知道相机的具体参数。 相机参数的确定过程 就叫做 相机的标定 。在双目视觉系统中，除了 对每个相机进行标定外 ， 还需要知道相机间的相互关系以及相机与待测物体的坐标关系 ，这一过程叫做 系统的标定 。

从图像上的物体到三维空间上的物体的映射过程实际上是坐标系的变换。 图像 上的某一点，经过物理关系的转换可以得到现实的物理坐标，然后将图像平面映射成 相机坐标系 的某一平面，得到该点在相机坐标系的坐标，最后通过相机坐标系与 世界坐标系 的旋转平移变换就可以确定该点的实际三维坐标了。所以要想确定点的三维坐标，首先要了解这四个坐标系。

像素坐标系

在数字图像中，一幅图像就是一个 \(M\) 行 \(N\) 列的数组，数组中的每个数值就是该点的亮度。在图像的左上角建立直角坐标系 \(u\)、\(v\)， 每一像素的坐标 \((u, v)\) 就是该像素在数组中的行和列。以像素作为单位的坐标系就叫做像素坐标系。

图像坐标系

要想知道物体在三维空间的具体位置，就需要建立与实际物理单位相关的坐标系，这样的坐标系叫做图像坐标系，该坐标系以图像内某一点作为坐标原点，其 \(x\) 轴和 \(y\) 轴分别与像素坐标系的 \(u\) 轴，\(v\) 轴平行。图像上任意一个像素在两个坐标系的映射关系为：

\[ \begin{cases} u=\frac{x}{dx}+u_0 \\ v=\frac{y}{dy}+v_0 \end{cases} \]

其中， 单个像素在 \(x\) 轴和 \(y\) 轴的实际物理距离为 \(dx\) 和 \(dy\) ，将上式转换成齐次方程式为：

\[ \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] = \left[ \begin{matrix} \frac{1}{dx} & 0 & u_0 \\ 0 & \frac{1}{dy} & v_0 \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right] \]

相机坐标系

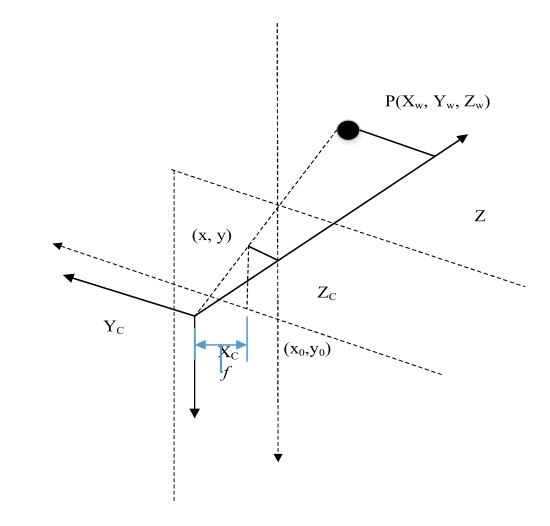
图像坐标系虽建立起图像与现实世界的物理关系，但这只是二维关系，因此，需要建立与三维世界相关的相机坐标系。图像坐标系是相机坐标系的某一平面，相机坐标系的 \(x\) 轴和 \(y\) 轴与图像坐标系对应轴平行 ， 两个坐标系间的距离就是相机的焦距 \(f\) 。其 以相机光心为坐标原点 ， 光轴为 \(z\) 轴 ，可以用 \((𝑋c, 𝑌c, 𝑍c )\) 来表示。

世界坐标系

相机坐标系是以相机为中心的描述现实世界的三维坐标系。在现实空间中，存在无数坐标系可以描述三维空间，为了确定三维空间点的具体位置，需要确定唯一一个基准坐标系来表述空间，这就是世界坐标系，用(𝑋w, 𝑌w, 𝑍w)来表示。

\[ \left[ \begin{matrix} X_c \\ Y_c \\ Z_c \\ 1 \end{matrix} \right] = \left[ \begin{matrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{matrix} \right] \left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \end{matrix} \right] \]

其中， R 为 3×3 单位正交矩阵，表示了坐标系的旋转操作；t 为三维平移向量，代表了坐标系的平移操作；0 表示三维零向量 。

坐标系转换公式

\[ \begin{aligned} s\left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] & = \left[ \begin{matrix} \frac{1}{dx} & 0 & u_0 \\ 0 & \frac{1}{dy} & v_0 \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{matrix} \right] \left[ \begin{matrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{matrix} \right] \left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \end{matrix} \right] \\ & = \left[ \begin{matrix} \alpha & \gamma & u_0 & 0 \\ 0 & \beta & v_0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right] \left[ \begin{matrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{matrix} \right] \left[ \begin{matrix} X_w \\ Y_w \\ Z_w \\ 1 \end{matrix} \right] \\ &= K\left[R,\mathbf{T}\right]X \end{aligned} \]

其中 \(s\) 为尺度因子，\(K\) 为摄像机内参数，\(R\) 为旋转矩阵，\(T\) 为平移向量 。

相机的畸变系数

上述的线性模型并不能准确描述物体与图像的对应关系，这是因为 光学镜头具有透视失真，会导致图像发生偏差，这是镜头的固有属性无法消除。 为了减少图像偏差，需要明确镜头的畸变系数，对图像进行校正。常见的畸变主要有 径向畸变 和 切向畸变 。

径向畸变

径向畸变是指图像像素以畸变中心为原点，沿着径向产生位置偏差，从而导致图像形变。其常用畸变原点周围的泰勒展开式的前两项 \(k1\) 和 \(k2\) 来表示，如果畸变较大，还可以增加使用第三项 \(k3\) 来描述，常用的描述公式为：

\[ \begin{cases} x_0=x(1+k_1r^2+k_2r^4+k_3r^6) \\ y_0=y(1+k_1r^2+k_2r^4+k_3r^6) \end{cases} \]

其中，\((x, y)\) 是校正后像素点的位置；\((𝑥_0, 𝑦_0)\) 是原图上的像素点位置；\(r\) 是径向距离。

切向畸变

切向畸变是由于在安装时，产生安装偏差，使镜头不完全平行于镜头平面而造成的畸变，其可以使用 \(p_1\) 和 \(p_2\) 两个参数来描述：

\[ \begin{cases} x_0=x+[2p_1xy+p_2(r^2+2x^2)] \\ y_0=y+[2p_2xy+p_1(r^2+2y^2)] \end{cases} \]

畸变参数

要消除镜头畸变，就是要同时消除径向畸变和切向畸变，所以要知道以下 5 个畸变参数的值：

\[ \text{Distortion\ Coefficients} = (k_1,k_2,p_1,p_2,k_3) \]

这 5 个参数可以在相机标定的过程中得到。明确这 5 个畸变系数 以及 相机的内外参数， 就可以完成相机的标定了。 #### 相机标定的分类

相机的标定是 根据像素坐标系与世界坐标系的关系，利用一定的约束条件，来求解相机的内外参数以及畸变系数的过程。 相机标定方法可分为两种，第一种是 需要参照物 的传统标定方法；另一种则是 不需参照物 的相机自标定法。

传统的标定方法一般以棋盘格作为参照物，其中每个棋盘格的大小，尺寸以及棋盘格的数量都是已知的。标定过程就是， 将棋盘格的顶点与图像上的对应点建立对应关系，利用棋盘格的已知信息来求得相机模型的内外参数和畸变系数。 这种标定方法通常有张正友标定法和 Tasi 两步标定法等。这种方法容易受到标定物的制作精度的影响，但 精度仍比另一种方法高 。

相机自标定法是不需要参照物的，通常有 基于 Kruppa 方程的标定法 等。其根据多视图约束几何方程，在不同位置采集多幅同场景的图像，通过相机的约束信息以及对 应点的几何信息来完成相机参数的计算。其最大优点就是不需要制作标定参考物，比较灵活；但由于缺少标定物，鲁棒性和精度都有所欠缺。

张正友标定法

”张正友标定”是指张正友教授1998年提出的单平面棋盘格的摄像机标定方法。文中提出的方法介于传统标定法和自标定法之间，但克服了传统标定法需要的高精度标定物的缺点，而仅需使用一个打印出来的棋盘格就可以。同时也相对于自标定而言，提高了精度，便于操作。因此张氏标定法被广泛应用于计算机视觉方面。

张正友标定法的基本步骤是：

1. 在不同角度下，对标定参考物（棋盘格）进行拍摄；
2. 然后提取出棋盘格的顶点；
3. 接着解析出相机的畸变系数和内外参数；
4. 最后再根据极大似然估计，对参数进行优化。

计算单应性矩阵 H

根据前文推出的坐标转换公式可知，设三维世界坐标的点为\(X=[X,Y,Z,1]^T\)，二维相机平面像素坐标为\(=M[u,v,1]^T\)，所以标定用的棋盘格平面到图像平面的单应性关系为：

\[ sM=K[R,T]X \]

其中 \(s\) 为尺度因子，\(K\) 为摄像机内参数，\(R\) 为旋转矩阵，\(T\) 为平移向量 。令

\[ K=\left[ \begin{matrix} \alpha & \gamma & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \end{matrix} \right]。 \]

注意，\(s\) 对于齐次坐标来说，不会改变齐次坐标值。张氏标定法中，将世界坐标系定义在棋盘格平面上，令棋盘格平面为 \(Z=0\) 的平面。则可得

\[ s\left[\begin{matrix}u \\ v \\ 1 \end{matrix}\right] = K\left[\begin{matrix}\mathbf{r_1} & \mathbf{r_2} & \mathbf{r_3} & \mathbf{t} \end{matrix}\right]\left[\begin{matrix}x \\ y \\ 0 \\ 1 \end{matrix}\right] = K\left[\begin{matrix}\mathbf{r_1} & \mathbf{r_2} & \mathbf{t} \end{matrix}\right]\left[\begin{matrix}x \\ y \\ 1 \end{matrix}\right] \]

我们把 \(K[r1,\ r2,\ t]\) 叫做 单应性矩阵 H ，即

\[ H=[h_1\ h_2\ h_3] = \lambda K[r_1\ r_2\ t] \]

\(H\) 是一个齐次矩阵，所以有8个未知数，至少需要8个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵 \(H\)。

计算内参数矩阵

由上式可得

\[ \lambda = \frac{1}{s} \\ r_1=\frac{1}{\lambda}K^{-1}h_1 \\ r_2=\frac{1}{\lambda}K^{-1}h_2 \]

由于旋转矩阵是个酉矩阵，\(r_1\) 和 \(r_2\) 正交，可得 约束条件 ：

\[ \begin{aligned} r_1^Tr_2=0 & \iff h_1^TK^{-T}K^{-1}h_2=0\\ ||r_1||=||r_2||=1 & \iff h_1^TK^{-T}K^{-1}h_1 = h_2^TK^{-T}K^{-1}h_2 \end{aligned} \]

即 每个单应性矩阵能提供两个方程，而内参数矩阵包含5个参数，要求解，至少需要3个单应性矩阵 。为了得到三个不同的单应性矩阵，我们使用至少三幅棋盘格平面的图片进行标定，通过改变相机与标定板之间的相对位置来得到三个不同的图片。

为了方便计算，定义如下：

\[ B=K^{-T}K^{-1}= \left[ \begin{array}{ccc} B_{11} & B_{12} & B_{13} \\ B_{21} & B_{22} & B_{23} \\ B_{31} & B_{32} & B_{33} \end{array} \right]= \left[ \begin{array}{ccc} \frac{1}{\alpha^2} & -\frac{\gamma}{\alpha^2\beta} & \frac{v_0\gamma-u_0\beta}{\alpha^2\beta} \\ -\frac{\gamma}{\alpha^2\beta} & \frac{\gamma^2}{\alpha^2\beta^2}+\frac{1}{\beta^2} & -\frac{\gamma(v_0\gamma-u_0\beta)}{\alpha^2\beta^2}-\frac{v_0}{\beta^2} \\ \frac{v_0\gamma-u_0\beta}{\alpha^2\beta} & -\frac{\gamma(v_0\gamma-u_0\beta)}{\alpha^2\beta^2}-\frac{v_0}{\beta^2} & \frac{(v_0\gamma-u_0\beta)^2}{\alpha^2\beta^2}+\frac{v_0}{\beta^2}+1 \end{array} \right] \]

可以看到，\(B\) 是一个对称阵，所以 \(B\) 的有效元素为六个，让这六个元素写成向量 \(\mathbf{b}\)，即

\[ \mathbf{b}=\left[ \begin{array}{cccccc} B_{11} & B_{12} & B_{22} & B_{13} & B_{23} & B_{33} \end{array} \right]^T \]

可以推导得到（引入了 \(v_{ij}\) 项作化简）：

\[ h_i^TBh_j = v^T_{ij} \mathbf{b} \\ v_{ij}=\left[ \begin{array}{cccccc} h_{i1}h_{j1} & h_{i1}h_{j2}+h_{i2}h_{j1} & h_{i2}h_{j2} & h_{i3}h_{j1}+h_{i1}h_{j3} & h_{i3}h_{j2}+h_{i2}h_{j3} & h_{i3}h_{j3} \end{array} \right]^T \]

利用 约束条件 可以得到：

\[ \left[ \begin{array}{c} v^T_{12} \\ (v_{11}-v_{22})^T \end{array} \right] \mathbf{b}=0 \]

通过上式，我们至少需要三幅包含棋盘格的图像，可以计算得到 \(B\) ，然后通过 Cholesky分解 ， 得到相机的内参数矩阵 \(K\) 。 ##### 计算外参数矩阵

由之前的推导，可得

\[ \begin{cases} &\lambda = \frac{1}{s}=\frac{1}{\|A^{-1}h_1\|}=\frac{1}{\|A^{-1}h_2\|} \\ &r_1 =\frac{1}{\lambda}K^{-1}h_1 \\ &r_2 =\frac{1}{\lambda}K^{-1}h_2 \\ &r_3 = r_1 \times r_2 \\ &t=\lambda K^{-1}h_3 \end{cases} \]

极大似然估计

上述的推导结果是基于理想情况下的解，但由于可能存在高斯噪声，所以使用最大似然估计进行优化。设我们采集了 \(n\) 副包含棋盘格的图像进行定标，每个图像里有棋盘格角点 \(m\) 个。令第 \(i\) 副图像上的角点 \(M_{ij}\) 在上述计算得到的摄像机矩阵下图像上的投影点为：

\[ \hat{m}(K,R_i,t_i,M_{ij}) = K[R|t]M_{ij} \]

其中 \(R_i\) 和 \(t_i\) 是第 \(i\) 副图对应的旋转矩阵和平移向量，\(K\) 是内参数矩阵。则角点 \(m_{ij}\) 的概率密度函数为：

\[ f(m_{ij})=\frac{1}{\sqrt{2\pi}}e^{\frac{-(\hat{m}(K,R_i,t_i,M_{ij})-m_{ij})^2}{\sigma^2}} \]

构造似然函数：

\[ L(A,R_i,t_i,M_{ij}) = \prod^{n,m}_{i=1,j=1}f(m_{ij})=\frac{1}{\sqrt{2\pi}}e^{\frac{-\sum^n_{i=1}\sum^m_{j=1}(\hat{m}(K,R_i,t_i,M_{ij})-m_{ij})^2}{\sigma^2}} \]

让 \(L\) 取得最大值，即让下面式子最小。这里使用的是多参数非线性系统优化问题的 Levenberg-Marquardt 算法 进行迭代求最优解。

\[ \sum^n_{i=1}\sum^m_{j=1} \| \hat{m}(K,R_i,t_i,M_{ij})-m_{ij} \|^2 \]

径向畸变估计

张氏标定法只关注了影响最大的径向畸变，数学表达式为：

\[ \hat u = u + (u-u_0)[k_1(x^2+y^2)+k_2(x^2+y^2)^2] \\ \hat v = v + (v-v_0)[k_1(x^2+y^2)+k_2(x^2+y^2)^2] \]

其中，\((u,v)\) 是理想无畸变的像素坐标，\((\hat{u},\hat{v})\) 是实际畸变后的像素坐标。\((u_0,v_0)\) 代表主点，\((x,y)\) 是理想无畸变的连续图像坐标， \((\hat{x},\hat{y})\) 是实际畸变后的连续图像坐标，\(k_1\) 和 \(k_2\) 为前两阶的畸变参数。由前一小节，\((\hat{u},\hat{v})\) 可通过下式求出

\[ \hat u = u_0 + \alpha \hat x + \gamma \hat y \\ \hat v = v_0 + \beta \hat y \]

将径向畸变的数学表达式化成矩阵形式：

\[ \left[ \begin{array}{cc} (u-u_0)(x^2+y^2) & (u-u_0)(x^2+y^2)^2 \\ (v-v_0)(x^2+y^2) & (v-v_0)(x^2+y^2)^2 \end{array} \right] \left[ \begin{array}{c} k_1 \\ k_2 \end{array} \right]= \left[ \begin{array}{c} \hat u -u \\ \hat v -v \end{array} \right] \]

记作

\[ D\mathbf{k}=\mathbf{d} \]

则可得

\[ \mathbf{k}=[k_1\ k_2]^T = (D^TD)^{-1}D^T\mathbf{d} \]

根据上式，计算得到畸变系数 \(k\) 。

使用最大似然的思想优化得到的结果，即像上一步一样，使用LM法计算使下列函数值最小的参数值：

\[ \sum^n_{i=1}\sum^m_{j=1} \| \hat{m}(K,k_1,k_2,R_i,t_i,M_{ij})-m_{ij} \|^2 \]

到此，张正友标定法介绍完毕。我们也得到了相机内参、外参和畸变系数。

双目相机的标定

对于双目视觉系统， 不仅要对每个相机进行标定，同时还要明确相机间的相互关系，因此还要对双目相机进行进一步的标定，即求取相机间的旋转矩阵和平移向量。 首先，根据前面的方法得到每个相机的外参：

\[ x_{left}=R_{left}X_w+t_{left} \\ x_{right}=R_{right}X_w+t_{right} \]

又因为双目视觉系统的左右两个相机满足下列关系式：

\[ x_{right}=R\cdot x_{left}+t \]

可以推出：

\[ R=R_{right}R_{left}^{-1} \\ t=r_{right}-R\cdot t_{left} \]

根据上式即可计算得到左右相机间的旋转矩阵 \(R\) 和 平移向量 \(t\) 。即 只需要知道每个相机的外参数，就可以求得双目相机的旋转矩阵和平移向量。 ------

图像匹配

前文讲到，对于左图的任一个点，沿着它在右图中水平极线方向寻找和它最匹配的像素点。但在实际进行像素点匹配的时候，情况往往更加复杂，比如：

1. 实际上要保证两个相机完全共面且参数一致是非常困难的，而且计算过程中也会产生误差累积，因此对于左图的一个点，其在右图的对应点不一定恰好在极线上，而是在极线附近，所以搜索范围需要适当放宽。
2. 单个像素点进行比较鲁棒性很差，很容易受到光照变化和视角不同的影响。

立体匹配的基本约束条件

• (1) 极线约束。 极线约束是最常用的约束条件。 极线约束是指在左图像中的一点，它在右图像上的 对应匹配点必定在某一条直线上，这条直线就是极线 。使用极线约束就可以让图像的搜索范围由二维下降至一维，只需要在一条直线上进行搜索，这就可以大大减少搜索的复杂度，并提高了匹配的精度。
• (2) 相似性约束。 在进行立体匹配时，点、线、块等元素一定具有相同或相似的属性。
• (3) 唯一性约束。 对于待匹配图像，在原图像中至多对应一个点。一幅图像上的每个点只能与另一幅 图像上的唯一一个点一一对应，这样 图像上的点至多有一个视差值 。
• (4) 左右一致性约束。 若左图像上的一点 P，其在右图像上的对应点为 Q，则右图像上的点 Q 在左图像上的对应点应该是点 P，如果这两点不是一一对应的，则匹配会不满足唯一性条件，说明匹配失败。

在进行立体匹配时， 运用基本约束条件对匹配结果进行检验，可以有效排除很多误匹配的点，减小搜索范围，降低立体匹配计算的复杂度，提高立体匹配的速度和精度， 获得最好的匹配效果。

基于滑动窗口的图像匹配

基于能量优化的图像匹配

参考文献

张正友标定算法原理详解_Sylvester的博客-CSDN博客_张正友标定法原理

单应性 - 维基百科，自由的百科全书 (wikipedia.org)

来聊聊双目视觉的基础知识（视察深度、标定、立体匹配） - 极术社区 - 连接开发者与智能计算生态 (aijishu.com)

双目深度估计中的自监督学习概览 | 机器之心 (jiqizhixin.com)

深度相机原理揭秘--双目立体视觉 (sohu.com)

双目立体视觉之深度估计_小小小富的博客-CSDN博客_双目深度估计