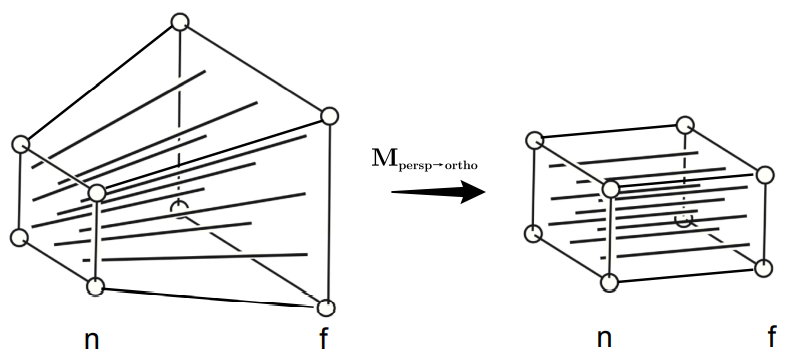
矩阵变换
总体流程
-
初始情况 :世界坐标系下的场景,场景中包含若干物体以及相机。
-
其中,相机包括 ①相机位置 pos;②向上方向 up;③朝向 look-at 三个参数。
-
view/camera 视图转换 :将相机转换到坐标系原点,且up为y轴正方向,look-at为z轴负方向。
-
该转换会应用于整个场景,不只是相机,即转换前后,相机在场景中的相对位置不变。
-
注意,不同渲染软件中相机转换到的位置以及参数可能不同,此处以GAMES-101中为例。
-
projection 投影转换 :将3维的视景体转换为标准立方体\([-1, 1]^3\)。
-
常见的有正交投影和透视投影两种投影变换方式,一般情况下使用透视投影的方法。
-
viewport 视窗转换 :将成像平面的xy平面从\([-1,1]^2\)转换为 $[0,width]×[0,height] $。
-
此时,z坐标无关紧要,可以理解为将立方体拍扁成二维正方形,再进行拉伸和平移。
-
视窗转换后的结果就是最终的照片,即将成像平面转换到屏幕坐标系下了。
视图转换
转换目标
如下图,将相机的 位置 \(\vec{e}\) 转换到原点, 向上方向 \(\hat{t}\) 转换到 \(y\) 轴正方向, 朝向 \(\hat{g}\) 转换到 \(z\) 轴负方向。
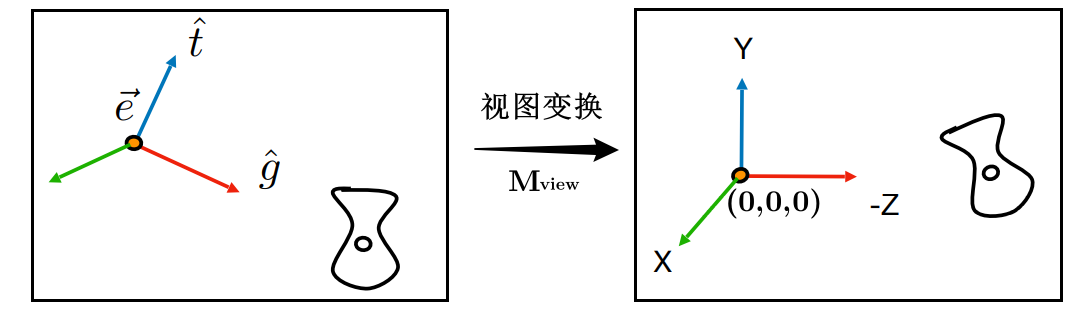
视图矩阵
视图转换的过程可以拆分为以下子过程,即 \(M_{view} = R_{view} \cdot T_{view}\): 第一步 ,将相机的位置 \(\vec{e}\) 转换到原点 \((0,0,0)\)
\[
T_{\text {view }}=\left[\begin{array}{cccc}
1 & 0 & 0 & -x_{e} \\
0 & 1 & 0 & -y_{e} \\
0 & 0 & 1 & -z_{e} \\
0 & 0 & 0 & 1
\end{array}\right]
\]
第二步 ,将朝向 \(\hat{g}\) 转换到\(z\)轴负方向,向上方向 \(\hat{t}\) 转换到\(y\)轴正方向, \(\hat{g} × \hat{t}\) 转换到\(x\)轴正方向
-
以 \(\hat{g}\) 为例,要将 \((x_{\hat{g}}, y_{\hat{g}}, z_{\hat{g}})\) 旋转到 \((0,1,0)\) 方向上,即求出旋转矩阵 \(R\) ,满足 \({R}\cdot (x_{\hat{g}}, y_{\hat{g}}, z_{\hat{g}})^T = (0,1,0)^T\) 成立,也就是 \((x_{\hat{g}}, y_{\hat{g}}, z_{\hat{g}})^T ={R}^{-1}\cdot (0,1,0)^T\)。
-
同理可以得到下列等式:
\[
\left[\begin{array}{cccc}
x_{\hat{g} \times \hat{t}} & x_{\hat{t}} & x_{\hat{g} } & 0 \\
y_{\hat{g} \times \hat{t}} & y_{\hat{t}} & y_{\hat{g} } & 0 \\
z_{\hat{g} \times \hat{t}} & z_{\hat{t}} & z_{\hat{g} } & 0 \\
0 & 0 & 0 & 1
\end{array}\right]=R_{\text {view }}^{-1} \cdot \left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\]
- 求解上式可以求出 $R^{-1}_{view} $ :
\[
R_{\text {view }}^{-1}=\left[\begin{array}{cccc}
x_{\hat{g} \times \hat{t}} & x_{\hat{t}} & x_{-\hat{g} } & 0 \\
y_{\hat{g} \times \hat{t}} & y_{\hat{t}} & y_{-\hat{g} } & 0 \\
z_{\hat{g} \times \hat{t}} & z_{\hat{t}} & z_{-\hat{g} } & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\]
- 对 \(R^{-1}_{view}\) 求逆矩阵,得到旋转矩阵 \(R_{view}\) :
\[
R_{\text {view }}=\left[\begin{array}{cccc}
x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\
x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0 \\
x_{-\hat{g} }& y_{-\hat{g} } & z_{-\hat{g} } & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\]
结合上述两个过程,可得到最终的 视图转换矩阵为
\[
M_{view}=R_{view}\cdot T_{view}=\left[\begin{array}{cccc}
x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\
x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0 \\
x_{-\hat{g} }& y_{-\hat{g} } & z_{-\hat{g} } & 0 \\
0 & 0 & 0 & 1
\end{array}\right] \cdot \left[\begin{array}{cccc}
1 & 0 & 0 & -x_{e} \\
0 & 1 & 0 & -y_{e} \\
0 & 0 & 1 & -z_{e} \\
0 & 0 & 0 & 1
\end{array}\right]
\]
投影转换
如下图所示,常见的投影转换有透视投影(perspective projection)和正交投影(orthographic projection)两种。透视投影的视景体为锥体,成像效果为近大远小;正交投影的视景体为长方体,成像效果为平行成像,远近一致。
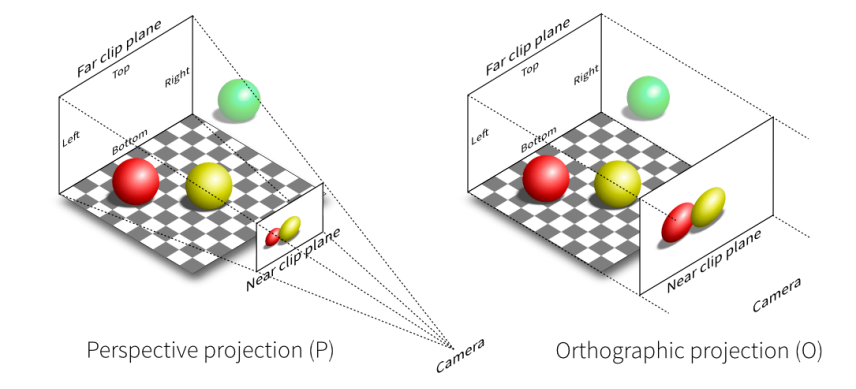
转换目标
对于正交投影来说,转换的目标是将视景体 \([l,r]×[b,t]×[f,n]\) 转换到标准立方体 \([-1,1]^3\)。
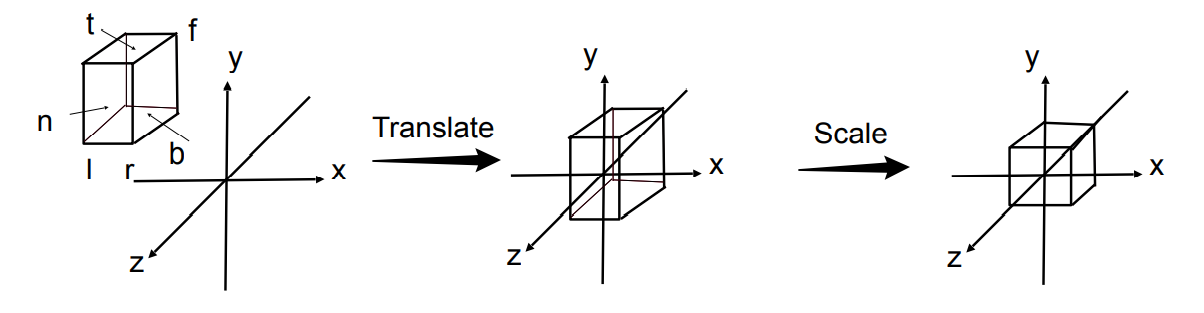
对于透视投影来说,投影转换的目标可以拆解为两步。第一步,将锥形视景体转换到长方体视景体;第二步,将长方形视景体转换到标准立方体(这一步与正交投影相同)。如下图所示。

投影矩阵
下面我们首先推导正交投影的视图矩阵 \(M_{ortho}\) ,然后推导将透视投影视景体转换为正交投影视景体的转换矩阵 \(M_{persp→ortho}\) ,最终得到透视投影的视图矩阵 \(M_{persp}=M_{ortho}\cdot M_{persp→ortho}\) 。
正交投影
正交投影可以分为两步:①将视景体中心移到原点;②将视景体缩放到标准立方体。易得
\[
M_{\text {ortho }}=\left[\begin{array}{cccc}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc}
1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1
\end{array}\right]
\]
透视投影
特别注意的是,在将视景体“压缩”成长方体时,我们规定了 三点原则 : Ⅰ. 近平面的所有点坐标不变; Ⅱ. 远平面的所有点的z轴坐标不变; Ⅲ. 远平面的中心点坐标不变。
透视投影也可以分为两步:①将锥形视景体“压缩”成长方体(\(M_{persp→ortho}\));②正交投影。 第一步 ,推导“压缩”矩阵。如下图所示,这里我们关注的是 \((x,y,z) → (x',y',z')\) 的过程。
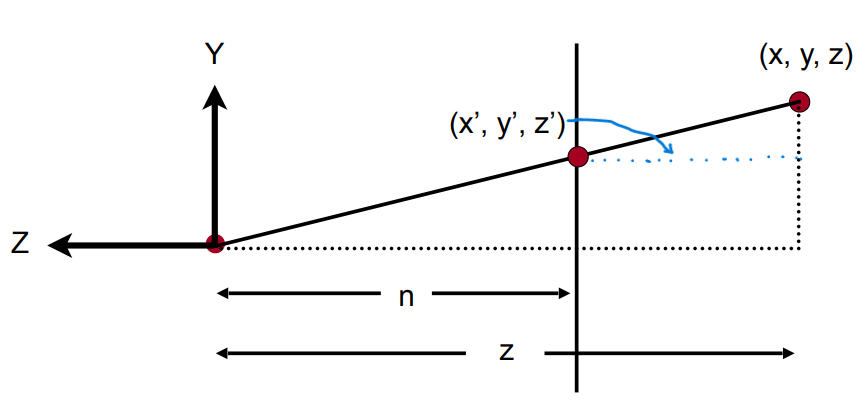
- 根据相似三角形法则与视景体转换的原则Ⅱ,结合右上图,得 \(x→x'\) 的关系式为 \(x'=\frac{n}{z} x\) ,同理可得 \(y→y'\) 的关系式为 \(y'=\frac{n}{z}y\) ,此时有等式:
\[
M_{p e r s p \rightarrow \text { ortho }}\cdot\left(\begin{array}{l}
x \\
y \\
z \\
1
\end{array}\right)=\left(\begin{array}{c}
n x/z \\
n y/z \\
\text { unknown } \\
1
\end{array}\right)==\left(\begin{array}{c}
n x \\
n y \\
\text { unknown } \\
z
\end{array}\right)
\]
注意:上式中用到了齐次坐标系下 \(k\vec{v}=\vec{v}\) 的定理,从而使求得的转换矩阵不包含变量 \(z\) 。
- 记 \(m_{ij}\) 为矩阵 \(M_{persp→ortho}\) 的第 \(i\) 行第 \(j\) 列的元素,根据上面的等式,有
\[
\begin{cases}
m_{11}\cdot x + m_{12}\cdot y + m_{13}\cdot z + m_{14}\cdot 1 = nx \\
m_{21}\cdot x + m_{22}\cdot y + m_{23}\cdot z + m_{24}\cdot 1 = ny \\
m_{41}\cdot x + m_{42}\cdot y + m_{43}\cdot z + m_{44}\cdot 1 = z
\end{cases}
\]
- 根据上面的等式,可以解出 $M_{persp→ortho} $ 的部分参数,得到
\[
M_{\text {persp→ortho}}=\left[\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
? & ? & ? & ? \\
0 & 0 & 1 & 0
\end{array}\right]
\]
- 根据视景体转换的原则Ⅰ,近平面的所有点的坐标不变,即对于任意的点 \((x,y,n,1)\) ,恒有 \(M_{persp→ortho}\cdot(x,y,n,1)^T=(x,y,n,1)^T\) 成立,得到
\[
\left[\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
? & ? & ? & ? \\
0 & 0 & 1 & 0
\end{array}\right] \cdot \left[\begin{array}{c}
x \\
y \\
n \\
1
\end{array}\right]=\left[\begin{array}{c}
x \\
y \\
n \\
1
\end{array}\right]==\left[\begin{array}{c}
nx \\
ny \\
n^2 \\
n
\end{array}\right]
\]
\[
m_{31}\cdot x+m_{32}\cdot y+m_{33}\cdot n+m_{34}\cdot 1=n^2
\]
- 上式并不足以解出参数,现考虑视景体转换的原则Ⅲ,远平面中心点的坐标不变且为 \((0,0,f)\),即有 \(M_{persp→ortho}\cdot (0,0,f,1)^T=(0,0,f,1)^T\) 恒成立,得到
\[
\left[\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
? & ? & ? & ? \\
0 & 0 & 1 & 0
\end{array}\right] \cdot \left[\begin{array}{c}
0 \\
0 \\
f \\
1
\end{array}\right]=\left[\begin{array}{c}
0 \\
0 \\
f \\
1
\end{array}\right]==\left[\begin{array}{c}
0 \\
0 \\
f^2 \\
f
\end{array}\right]
\]
\[
m_{31}\cdot 0+m_{32}\cdot 0+m_{33}\cdot f+m_{34}\cdot 1=f^2
\]
\[
\begin{cases}
m_{31}\cdot x+m_{32}\cdot y+m_{33}\cdot n+m_{34}\cdot 1=n^2 \\
m_{31}\cdot 0+m_{32}\cdot 0+m_{33}\cdot f+m_{34}\cdot 1=f^2
\end{cases}
\Rightarrow
\begin{cases}
m_{31}=m_{32}=0\\
m_{33}=n+f \\
m_{34}=-nf
\end{cases}
\]
- 到此,我们求出了将视景体“压缩”到长方体的转换矩阵:
\[
M_{\text {persp→ortho}}=\left[\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}\right]
\]
第二步 ,将长方形视景体转换到标准立方体,这一步与正交投影相同,根据前面的推导,有
\[
M_{\text {ortho }}=\left[\begin{array}{cccc}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc}
1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1
\end{array}\right]
\]
综上所述,我们得到最终的 透视投影矩阵 为
\[
\begin{aligned}
M_{persp} &= M_{ortho} \cdot M_{persp→ortho} \\ &= \left[\begin{array}{cccc}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc}
1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}\right]
\end{aligned}
\]
透视投影(补充)
上文讨论了视景体以参数 $[l,r]×[b,t]×[f,n] $ 形式表示时的透视投影矩阵,但是一般情况下,我们都是用 视场角 \(FOV\),宽高比 \(Apect\),远平面 \(Far\), 近平面 \(Near\) 四个参数来定义视景体的。
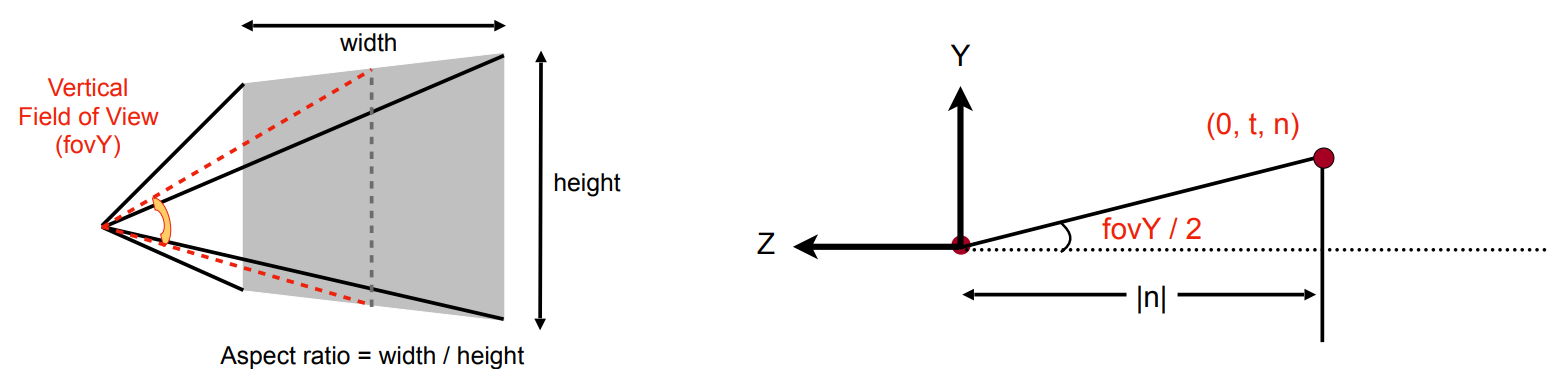
下面,推导一下用这四个参数表示时的透视投影矩阵。
\[
\begin{cases}
\tan {\frac{fovY}{2}}= \frac{t}{|n|} =\frac{-b}{|n|} \\
\tan {\frac{fovX}{2}}= \frac{r}{|n|}= \frac{-l}{|n|} \\
aspect=\frac{r}{t}=\frac{-l}{-b} \\
far=|f|,\ near=|n|
\end{cases}
\]
$$
- \begin{cases}
t = near\cdot \tan{\frac{fovY}{2}}=-b \
r=near\cdot \tan{\frac{fovX}{2}}= near\cdot \tan{\frac{fovY}{2}}\cdot aspect=-l \
n=-near, f=-far (far>near>0)
\end{cases}
$$
注意:由于相机视图转换时,我们将相机朝向设为 \(z\) 轴负方向,所以 \(n\) 和 \(f\) 均小于 \(0\) 。
\[
\begin{aligned}
M_{persp} &= \left[\begin{array}{cccc}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc}
1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}\right]\\ &=
\left[\begin{array}{cccc}
\frac{1}{near\cdot \tan{\frac{fovX}{2}}} & 0 & 0 & 0 \\
0 & \frac{1}{near\cdot \tan{\frac{fovY}{2}}} & 0 & 0 \\
0 & 0 & \frac{2}{far-near} & 0 \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & \frac{near+far}{2} \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc} -near & 0 & 0 & 0 \\
0 & -near & 0 & 0 \\
0 & 0 & -(near+far) & -near\cdot far \\
0 & 0 & 1 & 0
\end{array}\right] \\&=
\left[\begin{array}{cccc}
\frac{1}{near\cdot \tan{\frac{fovX}{2}}} & 0 & 0 & 0 \\
0 & \frac{1}{near\cdot \tan{\frac{fovY}{2}}} & 0 & 0 \\
0 & 0 & \frac{2}{far-near} & \frac{near+far}{far-near} \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc} -near & 0 & 0 & 0 \\
0 & -near & 0 & 0 \\
0 & 0 & -(near+far) & -near\cdot far \\
0 & 0 & 1 & 0
\end{array}\right]\\ &=
\left[\begin{array}{cccc}
\frac{-1}{\tan{\frac{fovX}{2}}} & 0 & 0 & 0 \\
0 & \frac{-1}{\tan{\frac{fovY}{2}}} & 0 & 0 \\
0 & 0 & \frac{-(near+far)}{far-near} & \frac{-2\cdot near\cdot far}{far-near} \\
0 & 0 & 1 & 0
\end{array}\right]\\ &=
\left[\begin{array}{cccc}
\frac{-1}{aspect\cdot \tan{\frac{fovY}{2}}} & 0 & 0 & 0 \\
0 & \frac{-1}{\tan{\frac{fovY}{2}}} & 0 & 0 \\
0 & 0 & \frac{-(near+far)}{far-near} & \frac{-2\cdot near\cdot far}{far-near} \\
0 & 0 & 1 & 0
\end{array}\right]
\end{aligned}
\]
综上所述,我们得到最终的 透视投影矩阵 为
\[
M_{persp}=\left[\begin{array}{cccc}
\frac{-1}{aspect\cdot \tan{\frac{fovY}{2}}} & 0 & 0 & 0 \\
0 & \frac{-1}{\tan{\frac{fovY}{2}}} & 0 & 0 \\
0 & 0 & \frac{-(near+far)}{far-near} & \frac{-2\cdot near\cdot far}{far-near} \\
0 & 0 & 1 & 0
\end{array}\right]
\]
视窗转换
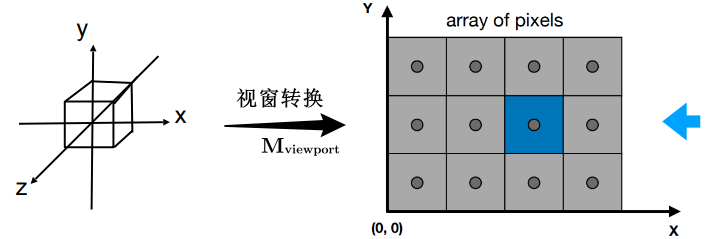
转换目标
通过上面的转换,我们已经得到了一个标准立方体 \([-1,1]\) ,下一步要做的就是视窗转换,即将标准立方体转换到 \([0,width] \times [0,height]\) 的平面(屏幕)上。如下图所示。
视窗矩阵
视窗转换可以拆解为两步:①缩放,即\([-1,1]\times[-1,1]→[-\frac{width}{2},\frac{width}{2}]\times[-\frac{height}{2},\frac{height}{2}]\) ②平移,即 \([-\frac{width}{2},\frac{width}{2}]\times[-\frac{height}{2},\frac{height}{2}] → [0,width]\times[0,height]\)。
综上所述,我们可以得到 视窗转换矩阵 为
\[
\begin{aligned}M_{viewport}&=
\left[\begin{array}{cccc}
1 & 0 & 0 & \frac{width}{2} \\
0 & 1 & 0 & \frac{height}{2} \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{cccc}
\frac{width}{2} & 0 & 0 & 0 \\
0 & \frac{height}{2} & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right]\\&=
\left[\begin{array}{cccc}
\frac{width}{2} & 0 & 0 & \frac{width}{2} \\
0 & \frac{height}{2} & 0 & \frac{height}{2} \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\end{aligned}
\]
总结
经过上面的推导,我们最终得到了将场景从初始的世界坐标系到屏幕坐标系的所有转换矩阵,如下 视图转换矩阵:
\[
M_{view}=\left[\begin{array}{cccc}
x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\
x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0 \\
x_{-\hat{g} }& y_{-\hat{g} } & z_{-\hat{g} } & 0 \\
0 & 0 & 0 & 1
\end{array}\right] \cdot \left[\begin{array}{cccc}
1 & 0 & 0 & -x_{e} \\
0 & 1 & 0 & -y_{e} \\
0 & 0 & 1 & -z_{e} \\
0 & 0 & 0 & 1
\end{array}\right]
\]
透视投影转换矩阵:
\[
\begin{aligned}
M_{persp} &= \left[\begin{array}{cccc}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc}
1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1
\end{array}\right]\left[\begin{array}{cccc}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}\right]\\
&=\left[\begin{array}{cccc}
\frac{-1}{aspect\cdot \tan{\frac{fovY}{2}}} & 0 & 0 & 0 \\
0 & \frac{-1}{\tan{\frac{fovY}{2}}} & 0 & 0 \\
0 & 0 & \frac{-(near+far)}{far-near} & \frac{-2\cdot near\cdot far}{far-near} \\
0 & 0 & 1 & 0
\end{array}\right]
\end{aligned}
\]
视窗转换矩阵:
\[
\begin{aligned}M_{viewport}=
\left[\begin{array}{cccc}
\frac{width}{2} & 0 & 0 & \frac{width}{2} \\
0 & \frac{height}{2} & 0 & \frac{height}{2} \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\end{aligned}
\]
对于初始世界坐标系下的场景坐标 $ (x,y,z) $ ,要将其最终呈现在屏幕上,即求其对应屏幕坐标系的点 \((x',y',z')\) ,只需要利用下列等式计算即可:
\[
(x',y',z',1)^T=M_{viewport}M_{persp}M_{view}(x,y,z,1)^T
\]
参考链接
GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibili
zhuanlan.zhihu.com
[图形学笔记]推导投影矩阵
OpenGL中的坐标变换、矩阵变换_孙群的博客-CSDN博客_ndc坐标系