体渲染方程
Volume Rendering for Developers: Foundations (scratchapixel.com)
简化方程¶
假设不考虑光在介质中的散射现象,则原辐射传输方程可以简化为:
\[
(\omega\cdot\nabla)L(\mathbf{x},\omega)=
\underbrace{-\sigma_a(\mathbf{x},\omega)L(\mathbf{x},\omega)}_{absorption}
+\underbrace{\sigma_a(\mathbf{x},\omega)L_e(\mathbf{x},\omega)}_{emission}
\]
对应地,渲染方程可以简化为(同时忽略背景颜色,即令 \(L(0)=0\)):
\[
L(\mathbf{x},\omega)=L(s)=\int^s_{t=0}T(t)\sigma_a(t)L_e(t)\mathrm{d}t,\quad T(s)=e^{-\int^s_{t=0}\sigma_a(t)\mathrm{d}t}
\]
离散化方程¶
上述积分式是无法在计算机中直接计算的,需要将其离散化才能求解。下面推导体渲染简化方程的离散求解式。
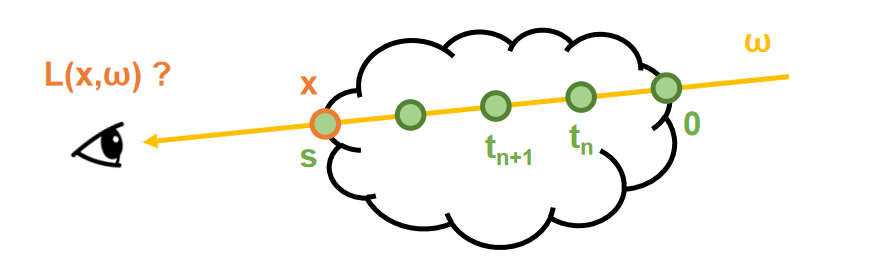
这里采用最简单的等距采样法,将整个光路 \([0,s]\) 划分为 \(N\) 个相等间距的区间 \([t_n,t_{n-1}]\),则有:
\[
L(t_n\to t_{n-1})=\int_{t=t_n}^{t_{n+1}}T(t)\sigma_a(t)L_e(t)\mathrm{d}t
\]
假设每个区间内的 \(\sigma\) 和 \(L_e\) 均不变,记为 \(\sigma_n\) 和 \(C_n\) ,则有:
\[
L(t_n\to t_{n-1})=\sigma_nC_n\int_{t=t_n}^{t_{n+1}}T(t)\mathrm{d}t
\]
进一步地,将 \(T(t)\) 拆分为两段的乘积形式:
\[
T(t)=e^{-\int^{t_n}_{0}\sigma_a(u)\mathrm{d}u}\cdot e^{-\int^t_{t_n}\sigma_a(u)\mathrm{d}u}=T(0\to t_n)\cdot T(t_n\to t)=T(t_n)\cdot T(t_n-t)
\]
相应地,区间内的辐射强度的积分式变为:
\[
\begin{aligned}
L(t_n\to t_{n+1})
&=\sigma_nC_n\int_{t=t_n}^{t_{n+1}}T(t_n)T(t_n\to t)\mathrm{d}t\\
&=\sigma_nC_nT(t_n)\int_{t=t_n}^{t_{n+1}}e^{-\int^{t}_{t_n}\sigma_n\mathrm{d}u}\mathrm{d}t\\
&=\sigma_nC_nT(t_n)\int_{t=t_n}^{t_{n+1}}e^{-\sigma_n(t-t_n)}\mathrm{d}t\\
&=\sigma_nC_nT(t_n)\frac{e^{-\sigma_n(t-t_n)}}{-\sigma_n}\mid^{t_{n+1}}_{t_{n}}\\
&=C_nT(t_n)(1-e^{-\sigma_n(t_{n+1}-t_n)})
\end{aligned}
\]
上式中的 \(T(t_n)\) 项仍是积分式,下面将其离散化,假设每个小区间长度为 \(\delta_n=t_{n+1}-t_{n}\) ,则有:
\[
T_n=T(t_n)=e^{-\int^{t_n}_{0}\sigma_a(u)\mathrm{d}u}\approx e^{-\sum_{k=1}^{n-1}\sigma_k\delta_k}
\]
由此得到区间内的辐射强度的离散表示:
\[
L(t_n\to t_{n+1})=C_nT_n(1-e^{-\sigma_n\delta_n}),\quad T_n=e^{-\sum_{k=1}^{n-1}\sigma_k\delta_k}
\]
最后,将所有采样区间的值累加得到 体渲染简化方程的离散表达 :
\[
L(\mathbf{x},\omega)=L(s)=\sum_{n=1}^{N}C_nT_n(1-e^{-\sigma_n\delta_n}),\quad T_n=e^{-\sum_{k=1}^{n-1}\sigma_k\delta_k}
\]