跳转至

辐射传输方程

Volume Rendering for Developers: Foundations (scratchapixel.com)

NeRF入门之体渲染 (Volume Rendering)

辐射传输方程

云、雾、浑浊的水等类似的介质可以散射光，换句话说，这些介质参与光的传输，故我们把此类介质称作 参与介质（participating media） 。

img

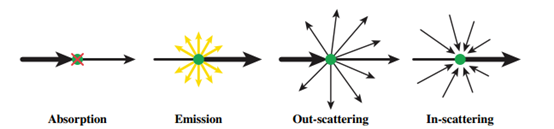
如果光在非真空中传播，我们有必要考虑环境中参与介质对光的传输的影响。如下图所示，狭窄（准直）光束穿过圆柱时，可以通过四种不同的方式与介质进行相互作用：

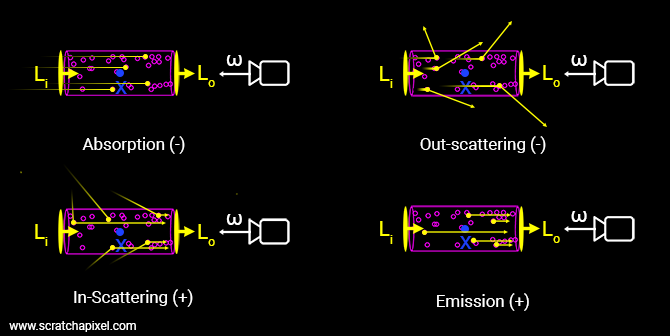
  • 吸收（Absorption） ：一些光被吸收转化成其他形式的能量，如热能。光束辐射强度降低。
  • 发射（Emission） ：气体在达到一定温度时会发射光。电子获得能量，以光子的形式释放出来。这些光子所取的方向是随机的，但最终其中一些将沿着光束的路径行进。光束辐射强度增加。
  • 外散射（Out-scattering） ：组成狭窄光束的光子朝向眼睛前进，但它们可能无法全部到达眼睛，因为其中一些会沿着另一个（随机的）方向散射开来。外部散射的光子不再在光束中，因此在这种情况下光束的辐射强度也会降低。
  • 内散射（In-scattering） ：散射也可能导致落在体积外的一些光被偏转到沿着我们光束的路径，使光束辐射强度增加。

img

上述物理现象在形式上可用如下的 辐射传输方程（Radiative Transfer Equation，RTE） 表示：

\[ \begin{aligned} (\omega\cdot\nabla)L(\mathbf{x},\omega)&= \underbrace{-\sigma_a(\mathbf{x},\omega)L(\mathbf{x},\omega)}_{absorption} \underbrace{-\sigma_s(\mathbf{x},\omega)L(\mathbf{x},\omega)}_{out-scattering} +\underbrace{\sigma_a(\mathbf{x},\omega)L_e(\mathbf{x},\omega)}_{emission} +\underbrace{\sigma_s(\mathbf{x},\omega)L_s(\mathbf{x},\omega)}_{in-scattering}\\ &= \underbrace{-\sigma_t(\mathbf{x},\omega)L(\mathbf{x},\omega)}_{extinction} +\underbrace{\sigma_a(\mathbf{x},\omega)L_e(\mathbf{x},\omega)}_{emission} +\underbrace{\sigma_s(\mathbf{x},\omega)L_s(\mathbf{x},\omega)}_{in-scattering} \end{aligned} \]

方程左侧是光线的辐射强度 \(L(\mathbf{x},\omega)\) 在 \(\mathbf{x}\) 点处沿 \(\mathbf{ω}\) 方向的变化量。右侧表示了各种物理作用对其的贡献，其中 \(\sigma_a(\cdot)\) 是吸收函数， \(\sigma_s(\cdot)\) 是散射函数，\(\sigma_t(\cdot)=\sigma_a(\cdot)+\sigma_s(\cdot)\) 是消光函数； \(L_e(\mathbf{x},\omega)\) 是在 \(\mathbf{x}\) 点处的粒子沿 \(\mathbf{ω}\) 方向发射的辐射强度； \(L_s(\mathbf{x},\omega)\) 是在 \(\mathbf{x}\) 点处的粒子接收到的来自四面八方的总辐射强度，其计算式如下，其中 \(p(\cdot)\) 是内散射的相函数（Phase function），它描述的是介质中某个点的散射在各个立体角方向上的分布情况。

\[ L_s(\mathbf{x},\omega)=\int_{\Omega}{p(\mathbf{x},\omega',\omega)L(\mathbf{x},\omega') \mathrm{d}\omega' } \]

为什么吸收项与发射项的系数相同

在辐射传输中，光线穿过介质时会与介质中的分子或原子相互作用。这个相互作用可以导致光子被吸收或发射。吸收和发射的过程是量子力学中的基本过程，它们的概率同时受到介质中分子或原子的能级结构的影响。 在量子力学的框架下，吸收和发射是对称的过程，即一个分子或原子吸收光子的概率和它发射光子的概率是相等的。因此，在一般情况下，辐射传输方程中的吸收和发射项系数是相等的。 当然，在某些特殊情况下，如非平衡态介质中，吸收和发射的过程可能不再是对称的，这时吸收项和发射项的系数就会有所不同。类似的，内散射项与外散射项系数也是相同的。

体渲染方程

体渲染的示意图如下，可以看出，体渲染方程是辐射传输方程在光照传输路径上的积分形式。

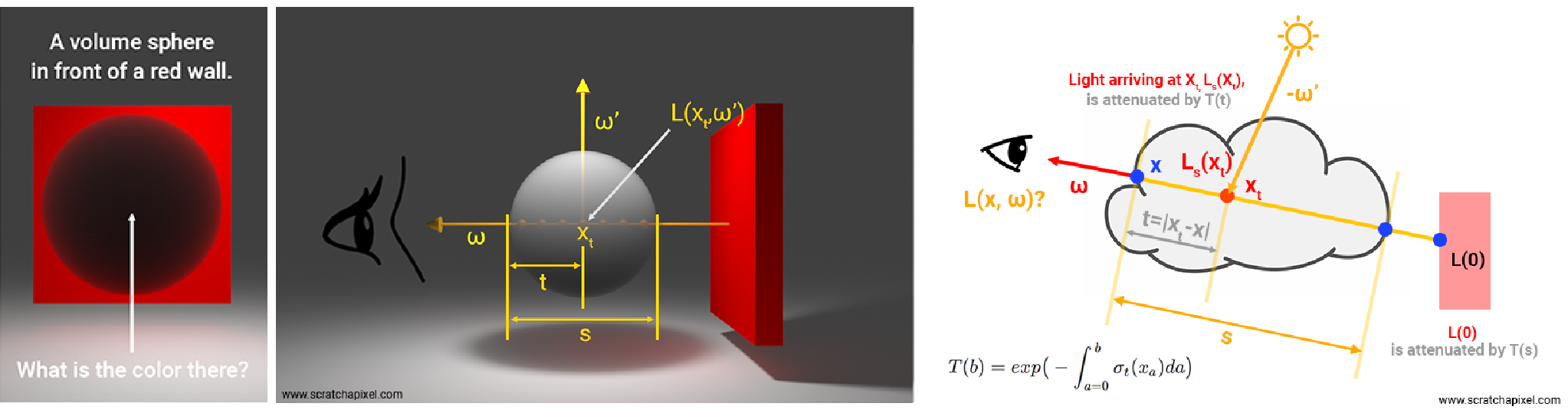
image-20230512215430704

具体地，我们重新定义辐射函数为距离 \(s\) 的函数，即 \(L(\mathbf{x},\omega)\to L(s)\)，原辐射传输方程表示为：

\[ \frac{\mathrm{d}L}{\mathrm{d}s}=-\sigma_t(s)L(s)+\sigma_a(s)L_e(s)+\sigma_s(s)L_s(s) \]

这是典型的一阶非齐次线性微分方程，形式为：

\[ y'+p(x)y=q(x)\\ \implies y(x)=e^{-\int{p(x)}\mathrm{d}x}(\int{e^{-\int{p(x)}\mathrm{d}x}q(x)\mathrm{d}x}+C) \]

相应地，求解这个微分方程，就可以得到 体渲染方程 ：

\[ L(s)=\int^s_{t=0}e^{-\int^t_{q=0}\sigma_t(q)\mathrm{d}q}[\sigma_a(t)L_e(t)+\sigma_s(t)L_s(t)]\mathrm{d}t+L(0)e^{-\int^s_{t=0}\sigma_t(t)\mathrm{d}t} \]

透射比

从辐射传输方程我们可以知道，入射光在经过介质 (粒子群) 后，辐射强度会衰减，且衰减速度与介质的性质有关。人们定义了透射比这个物理量来表征这一性质。具体地，透射比是介质入射光在入射点与出射点的辐射强度的比值。

根据透射比的定义，可以得到其表达式为

\[ T(a\to b)=\frac{L(b)}{L(a)}=\frac{L(0)e^{-\int^b_{t=0}\sigma_t(t)\mathrm{d}t}}{L(0)e^{-\int^a_{t=0}\sigma_t(t)\mathrm{d}t}}=e^{-\int^b_{t=a}\sigma_t(t)\mathrm{d}t} \]

因此，我们得到了 最终的体渲染方程 为

\[ L(s)=\int^s_{t=0}T(t)[\sigma_a(t)L_e(t)+\sigma_s(t)L_s(t)]\mathrm{d}t+L(0)T(s),\quad T(s)=T(0\to s)=e^{-\int^s_{t=0}\sigma_t(t)\mathrm{d}t} \]