点云转体素
Point Cloud to Volume¶
输入输出数据¶
- 输入数据
- 点云 point cloud:
(x,y,z)表示点在相机或世界坐标系下的三维坐标。 - 输出数据
- 体素网格 volume:
(i,j,k)表示点在体素网格中的索引坐标。
转换矩阵¶
从点云到体素的转换任务可以用下面的表达式来概括,即 将连续的三维坐标离散化为固定尺寸的体素网格索引 。
\[
(x_{min},x_{max})\times(y_{min},y_{max})\times(z_{min},z_{max})\quad \to \quad (0,W)\times(0,H)\times(0,D)
\]
有很多方式完成这种映射,下面仅介绍在本文的实践中采用的方法。
- 给定点云的包围盒 bbox,先将点云坐标归一化到 \((-1, 1)^3\) ,下图以二维为例。
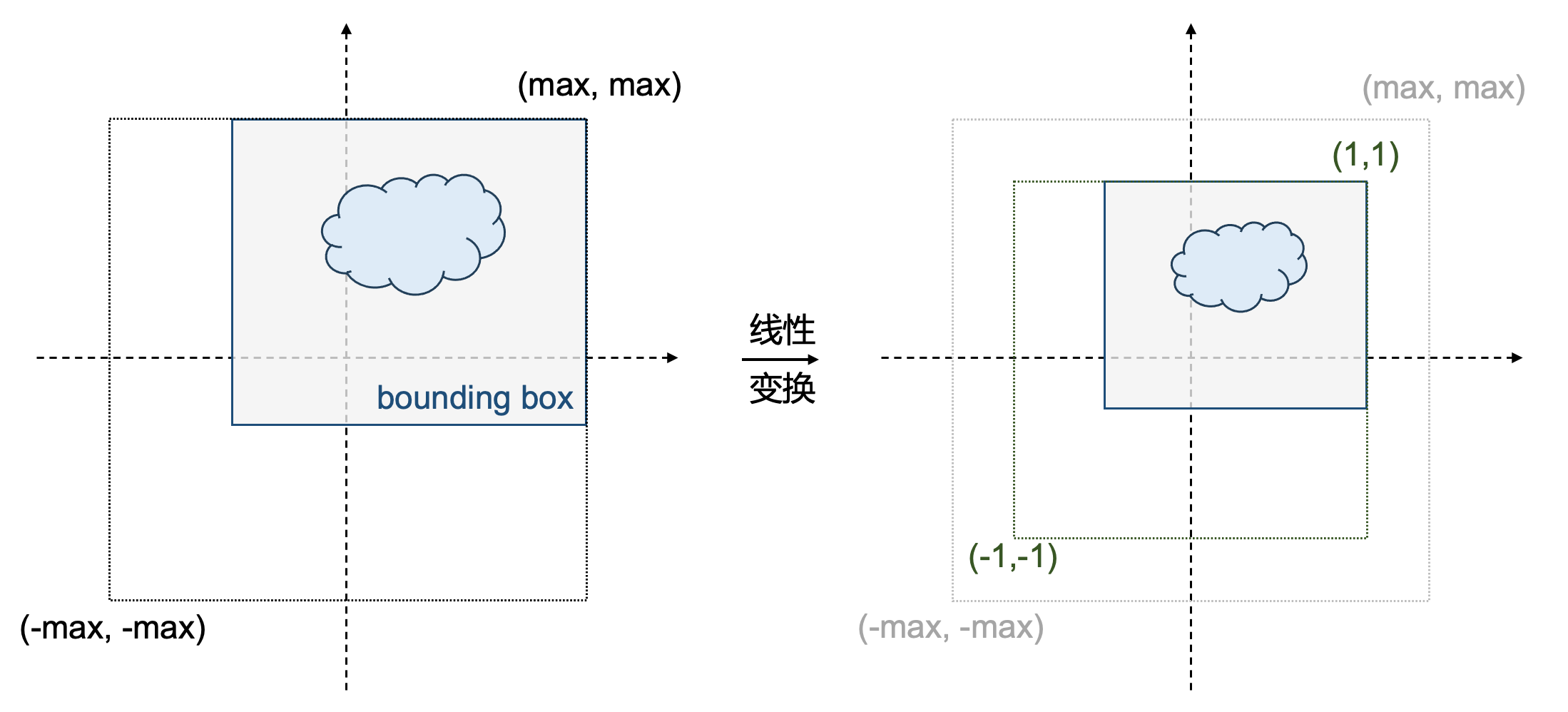
\[
\textcolor{blue}{\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}=\frac{1}{max}\begin{pmatrix}x \\ y \\ z\end{pmatrix}},
\quad\mathbf{where}\ \
max=\mathrm{max}(\mathrm{abs}(\mathbf{bbox}))
\]
- 给定体素的形状 \((H,W,D)\) ,将坐标由 \((-1, 1)^3\) 转换为 \((0,W)\times(0,H)\times(0,D)\) ,下图依然以二维为例。
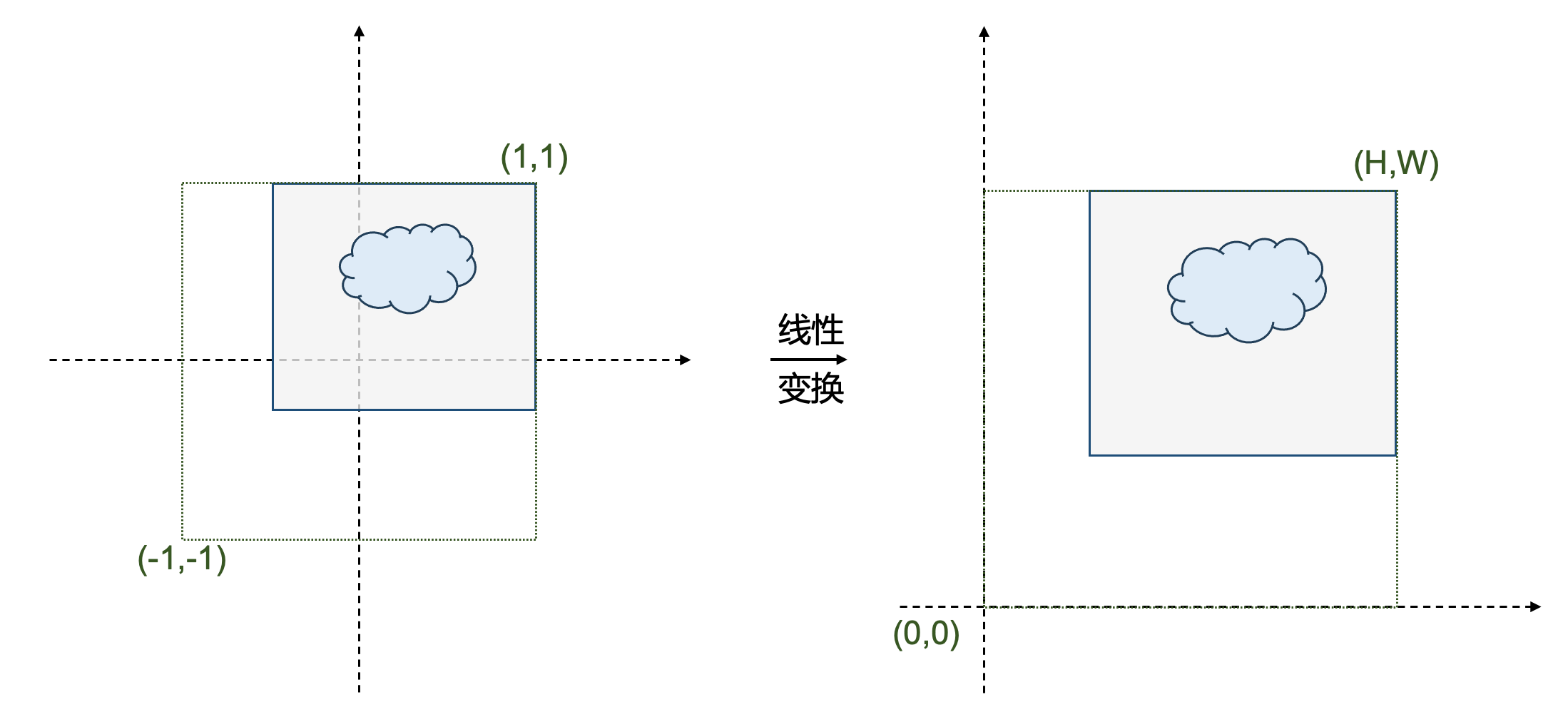
\[
\begin{pmatrix}x'' \\ y'' \\ z''\end{pmatrix}=\begin{pmatrix}W/2 &0 & 0\\ 0 & H/2 & 0 \\ 0 & 0 & D/2\end{pmatrix}\begin{bmatrix}\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}+\begin{pmatrix}1 \\ 1 \\ 1\end{pmatrix}\end{bmatrix}
\quad\Rightarrow\quad \textcolor{blue}{
\begin{pmatrix}x'' \\ y'' \\ z'' \\ 1\end{pmatrix}=\frac{1}{2}\begin{pmatrix}W &0 & 0 & W\\ 0 & H & 0 & H \\ 0 & 0 & D & D \\ 0 & 0 & 0 & 1\end{pmatrix}\begin{pmatrix}x' \\ y' \\ z' \\ 1\end{pmatrix}
}
\]