Dual Octree Graph Networks for Learning Adaptive Volumetric Shape Representations¶
概要¶
Key Ideas¶
- 使用八叉树来表示点云和体素网格 。
- 根据占有率对空间做自适应划分。
- 通过图网络在对偶八叉树图上做特征学习 。
- 原有的三维卷积方法是对同一分辨率的特征做卷积,而八叉树中每一个特征与其领域的特征分辨率有可能是不同的,因此引入图网络进行特征学习。
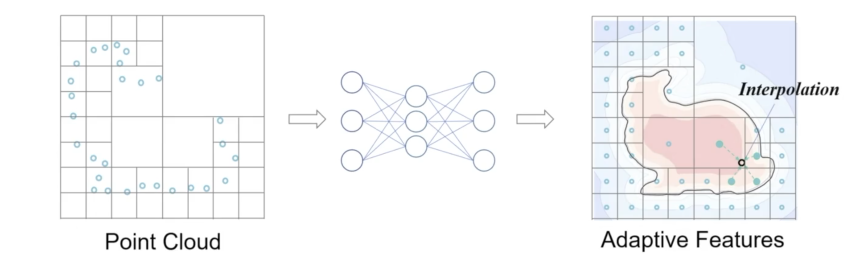
Dual Octree Graph¶
- 八叉树 :给定一个3D形状,可以通过对其占用空间与八叉树节点相交的节点进行递归细分来构建八叉树,直到达到指定的最大树深度。八叉树在接近表面处分配更细的体素,而在表面远离处分配更粗的体素。八叉树的叶节点形成了3D体积的完整分区。
- 对偶八叉树图 :八叉树的对偶八叉树图是通过 连接具有不同分辨率的所有面相邻(face-adjacent)的八叉树叶节点形成的 。
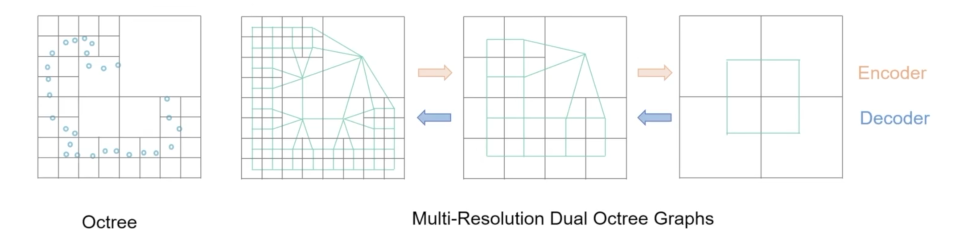
Graph Convolution on Dual Octrees¶
- Message passing 图卷积 :如下图所示,对任意一个点 \(i\),取其领域的所有点 \(N_{i}\),记点 \(i\) 和点 \(j\) 的偏差为 \(\Delta{p_{ij}}\) ,定义权重函数 \(W(\cdot)\), \(F_{i}\) 表示 \(i\) 点的特征值,则 message passing 的过程可表示为 \(F_i=\sum_{j\in N_i}W(\Delta p_{ij})\times F_j\) 。

- 本文提出的图卷积 :对偶八叉树图中各结点的位置关系 \(\Delta p_{ij}\) 只有有限个值,即权重函数 \(W(\cdot)\) 的定义域和值域都是有限的,因此,作者直接将权重函数 \(W(\Delta p_{ij})\) 定义为一个矩阵 \(W\)。如下图所示,将 \(\Delta p_{ij}\) 的取值简化为 上下左右前后与自身 七个取值。
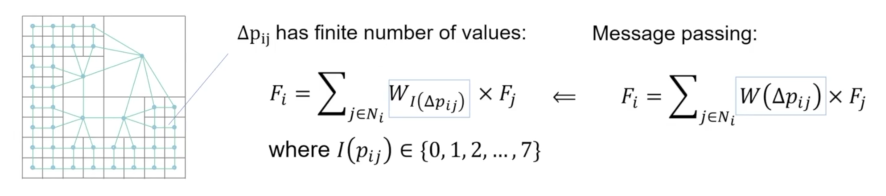
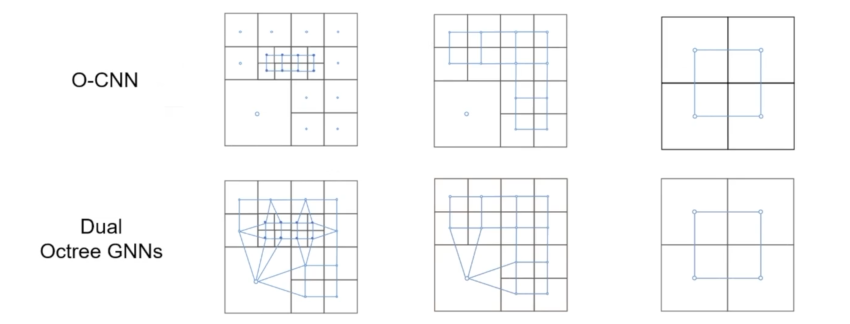
Multiscale Features in Convolutions¶
- 本文提出的图卷积结构的优越性 : 多尺度的特性 。一般的三维稀疏卷积,每次卷积操作都是对同一分辨率的特征做运算,如O-CNN;而Duel O-GNN每一次运算时不同分辨率的特征都参与了运算,扩大了感受野,具有更强的全局性。
详解¶
动机¶
三维几何的 体积场 (Volumetric field)表示,如SDF、occupancy field,被广泛地应用于三维建模与重建任务,最近也在基于学习的算法中体现出优势。然而,开发一种有效的神经体积场表示方法以及相应的三维形状生成和重建的学习方案(learning scheme)仍然是一个悬而未决的问题。
已有的方案主要有以下几种,
-
Full-Voxel-based CNNs 是2D图像域的操作到3D空间域的自然拓展,但存储与计算效率低;
-
Sparse-Voxel-based CNNs 仅关注非空的体素,提高了效率,但很难输出连续曲面(特别是对于真实场景的输入,如残缺点云数据),这是因为预测空体素的位置本身对于三维形状生成和重建任务来说就是个难问题。
-
Coordinate-based MLPs 使用单个MLP表示场景/物体的位置与场值的连续映射,但很难设计对应的编码网络进行学习,对于任一新场景需要重新训练MLP。
-
Hybrid Methods 把体素与MLP两种表示结合,具有一定的优势。
-
部分算法仍然没有设计有效的编码网络,对于新场景需要重新优化网络参数。
-
体素场的编码网络仍然是基于 Full-Voxel-based CNNs 或 Sparse-Voxel-based CNNs。 论文的关键思想 是使用自适应八叉树来表示点云和体积场,并在对偶八叉树图上用图网络学习特征。相比Full-Voxel方法效率有所提高,相比Sparse-Voxel方法可以保证全局特征聚合与连续的输出。
方法¶
论文提出的模型的输入为点云数据,首先基于点云数据划分八叉树,然后连接相邻的叶子节点得到对偶八叉树图(Dual Octree Graph),经过编码-解码网络,预测各叶子节点的特征,最后经过Neural MPU的方法插值得到任一查询点的场值。论文的核心创新点,是提出了基于对偶八叉树的图卷积算子,以及提出了Neural MPU的表示方法。可以高效地学习全局特征,保证输出的空间连续性。

Dual Octree Graph¶
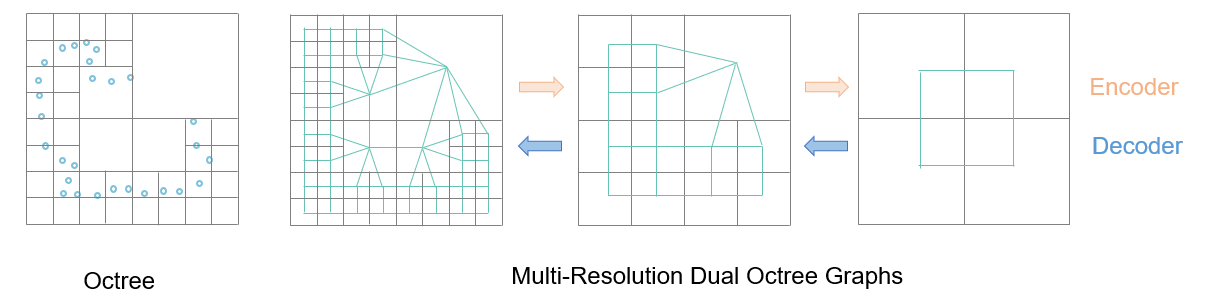
给定一个3D形状,可以通过递归细分其占用空间与形状相交的八叉树节点来构建八叉树,直到达到指定的最大树深度。八叉树在表面附近分配较细的体素,在表面以外分配较粗的体素。八叉树的叶节点构成三维体的完整分区。如下图所示。
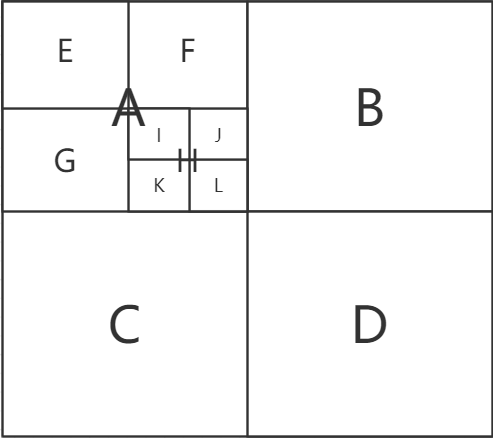 |
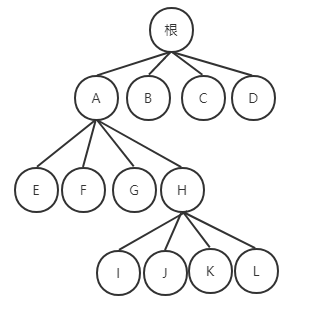 |
|---|---|
现有方法大多数是对八叉树的同一层的非空叶子节点做特征聚合/卷积运算,作者认为这类方法可能会导致空间不连续的体积场推断,感受野较小,因此,作者引入了对偶八叉树图结构。简单来说,将八叉树的相邻叶子节点连接后得到的图,就是对偶八叉树图。具体地,论文提出了一种可以用GPU加速的对偶八叉树图构建算法。如下图所示,八叉树深度+1后,原来的边会加倍,同时兄弟节点间也会形成新边。
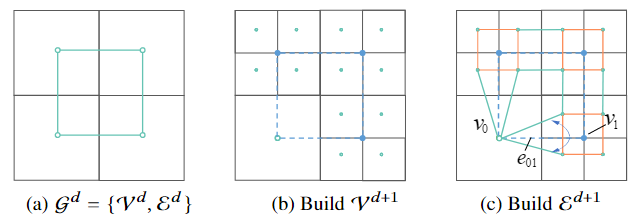
Dual Octree Graph CNNs¶
图卷积运算以图 \(\mathcal{G}=\{\mathcal{V},\mathcal{E}\}\) 和节点特征 \(F=\{F_i\}\) 作为输入,聚合(aggregate)邻居节点与本节点信息并更新 \(F\) 。以公式的形式表示如下。
其中,\(\mathcal{A}\) 是可微分的聚合算子(如累加、平均、最值)等;\(W(\cdot)\) 是一个权重函数,自变量为同一条边的两个图节点的相对位置 \(\Delta p_{i j}\) ,因变量为对应的卷积权重;\(\mathcal{N}_i\) 是点 \(v_i\) 的所有邻居节点。
现有方法通常将 \(W(\cdot)\) 定义为连续函数,如MLPs,这类权重函数会带来较大的计算开销。基于对偶八叉树图的特点,作者做了大胆的简化,将相邻节点的相对位置 \(\Delta p_{ij}\) 简化为 \(\{+x,-x,+y,-y,+z,-z,self\}\) 共7种,进而将 \(W(\cdot)\) 定义为7维矩阵,每一维对应了一种相对位置。通过这一简化,作者进一步地将整个图的卷积转化为矩阵运算,极大地提高了卷积效率。
上式为论文提出的聚合算子,式中 \(D_j\) 为节点 \(v_i\) 的八叉树深度 \(d_j\)的独热编码,\(I(\cdot)=\{0,...,6\}\)。
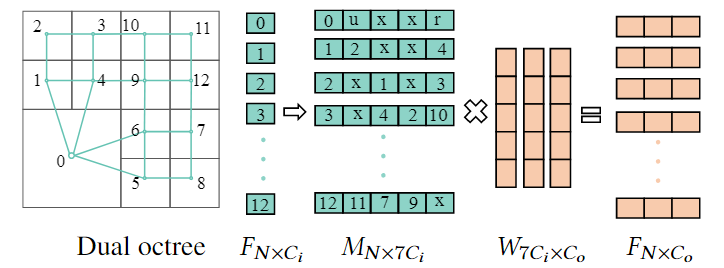
上图所示为论文提出的图卷积运算的二维示例(注意二维空间中相对位置退化为5种)。图中的 \(u\) 和 \(r\) 分别表示 0号节点上方和右方的所有节点特征的加和,\(x\) 表示该方向无邻居节点。
Neural MPU¶
上述的方法可以提取每个八叉树节点的特征,但最终目标是获得逐点(point-wise)的预测。因此,作者引入 multi-level partition of unity(MPU)插值方法。
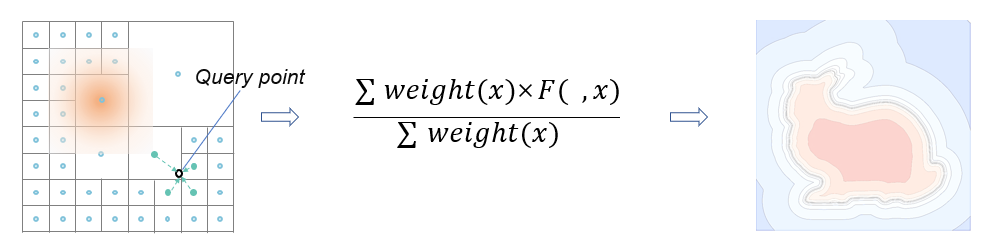
具体地,给定提取的节点特征集合 \(F^d=\{F_i\}\) ,对于 每个 八叉树叶子节点,论文定义了 MLP \(\Phi(x,F_i)\) ,其输入为查询点的坐标 \(x\) 和节点特征 \(F_i\) ,输出为局部函数值;定义了局部的融合权重函数 \(w_i(x)\) 和置信度 \(c_i\) 。因此,MPU的公式表达如下。
式中 \(F(x)\) 是一个全局连续可微的函数,权重函数 \(w_i(x)\) 的定义如下,其中 \(o_i\) 和 \(r_i\) 分别为节点体素的中心坐标与空间大小,\(c_i\) 是体素空间体积的倒数。\(B(\cdot)\) 保证了查询的局部性。
Network and Loss¶
基于前面所说的组件,作者提出了下图所示的U-Net结构。网络输入为深度为6的对偶八叉树图,在每一层Decoder后面都接了一个PredictionModule模块,用以预测上采样时的细分节点。
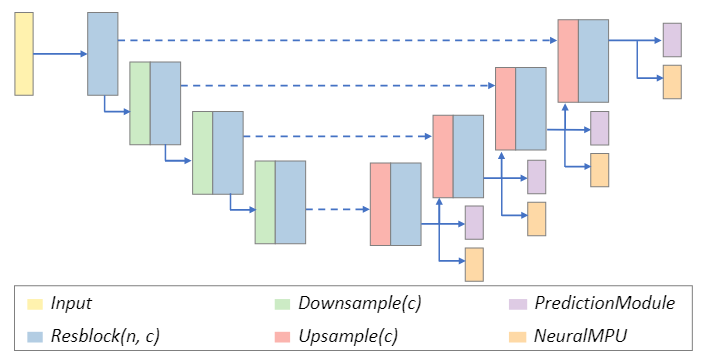
Downsample和Upsample模块对应了对偶八叉树图的下采样和上采样操作。具体地,下采样操作是将最深的一层叶子节点合并的操作(即树的深度减一),上采样则相反。如下图所示。
PredictionModule 模块所使用的 Loss 类似于二分类的 Loss:
NeuralMPU 模块所使用的 Loss 类似于 L2 Loss:
对于无监督学习来说,可以使用类似于泊松重建的梯度Loss:
实验¶
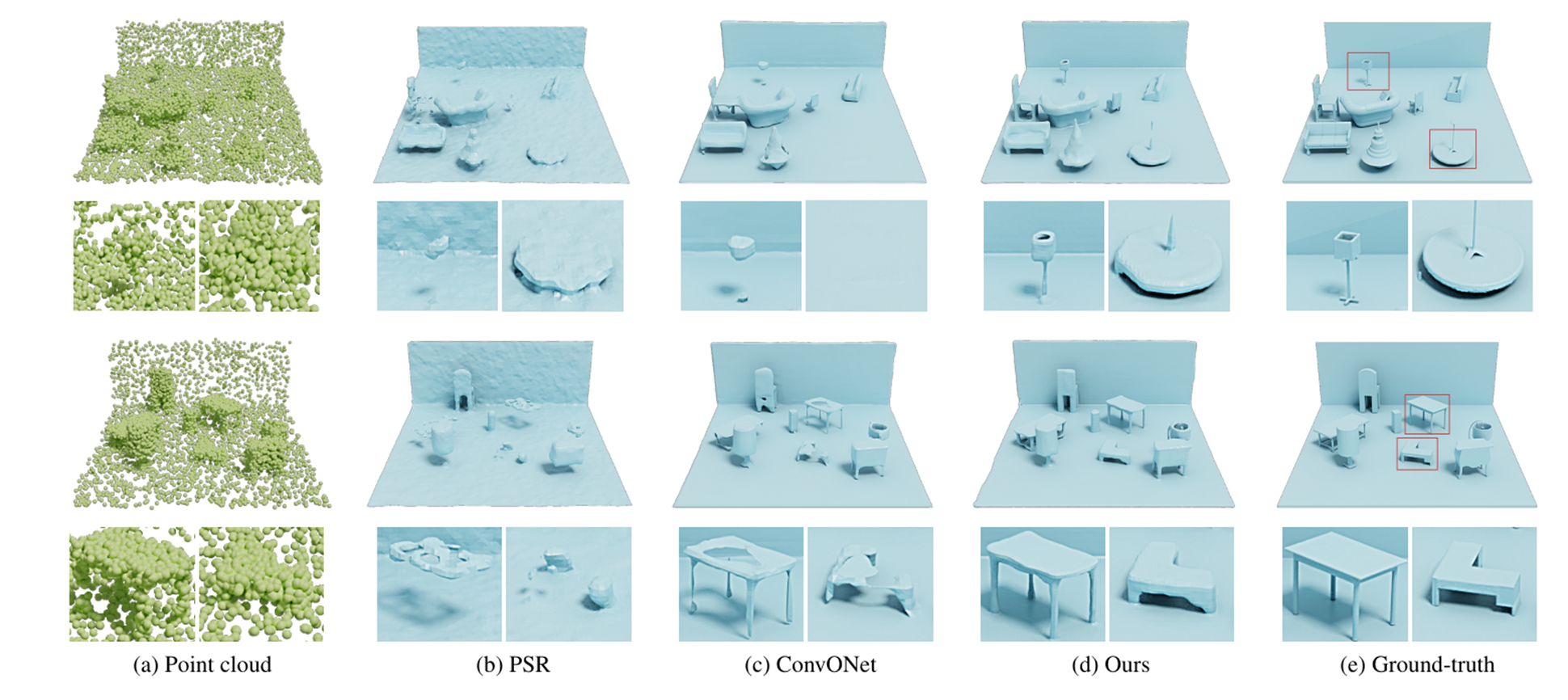
评价¶
论文的主要贡献是引入对偶八叉树图结构,设计了新的图卷积算子,可以更好地提取特征,结合Nerual MPU得到空间连续的输出结果。论文通过系列实验验证了这一贡献。